Предисловие
Думаю о ремонте. Изучил виды потолочных карнизов. Есть карнизы из полиуретана, полистирола и гипса. Карнизы из гипса мне нравятся больше всего. Они не горючие, из проверенного материала, нравится внешний вид и понятно как с ним работать. Карнизы из полиуретана выглядят сносно, но нравятся гораздо меньше. Теперь про цены. Анализировал первые попавшиеся ссылки из поисковика.
Полиуретан - от 212 (200 на 200) за м.п. Гипсовые - от 350 (40 на 40 мм) за м.п. Полистирол не рассматривал.
Цена карниза, который мне нравится и подходит по габаритам комнаты примерно 2 000 рублей за погонный метр. Мне нужно примерно 50 погонных метров на квартиру. Итого от 100 000 р. Мешок гипса (40 кг) стоит в районе 2 000 р. На один 1.5 м карниз уходит примерно 3 литра (будем считать кг 2.8 кг). Это около 14 карнизов. То есть нужно 3 мешка по 40 кг на 42 карниза и ещё мешок 25 кг на остальные 8. 25 кг мешок стоит около 1 200 р. Итого 7 200 за материалы. Работа по изготовлению сложно поддаётся оценке, так как нет опыта. Но я уже сделал 4 штуки и делать два карниза в день выглядит как задача минимум. Думаю при определённой сноровке можно сделать и 10 в день.
Экономика не в мою пользу. Кажется, что надёжнее заказать готовые изделия и смонтировать. Но я хочу в квартире сделать несколько вещей своими руками. Первая вещь это двери. Одну дверь я уже ошкурил от старой краски и перекрасил и теперь хочу сделать карнизы.
Сделать самому
Я ничего не придумывал сам, изучая варианты я наткнулся на видео, в которых ребята делают карнизы из гипса, некоторые делают на объекте, где проходит ремонт. Я решил заказать тестовую партию гипса и протянуть карниз самостоятельно.
Описание процесса
Для изготовления карниза из гипса нам понадобится:
1) Стол-верстак
2) Гипс Г16 (Самарский)
3) Каретка
4) Станок
5) Шаблон 1 под куклу, второй под карниз
6) Кукла - подложка для экономии гипса и облегчения протяжки
7) Нитро лак
8) Силиконовая смазка
9) Ёмкости для приготовления гипса
10) Ёмкости для нанесения гипса
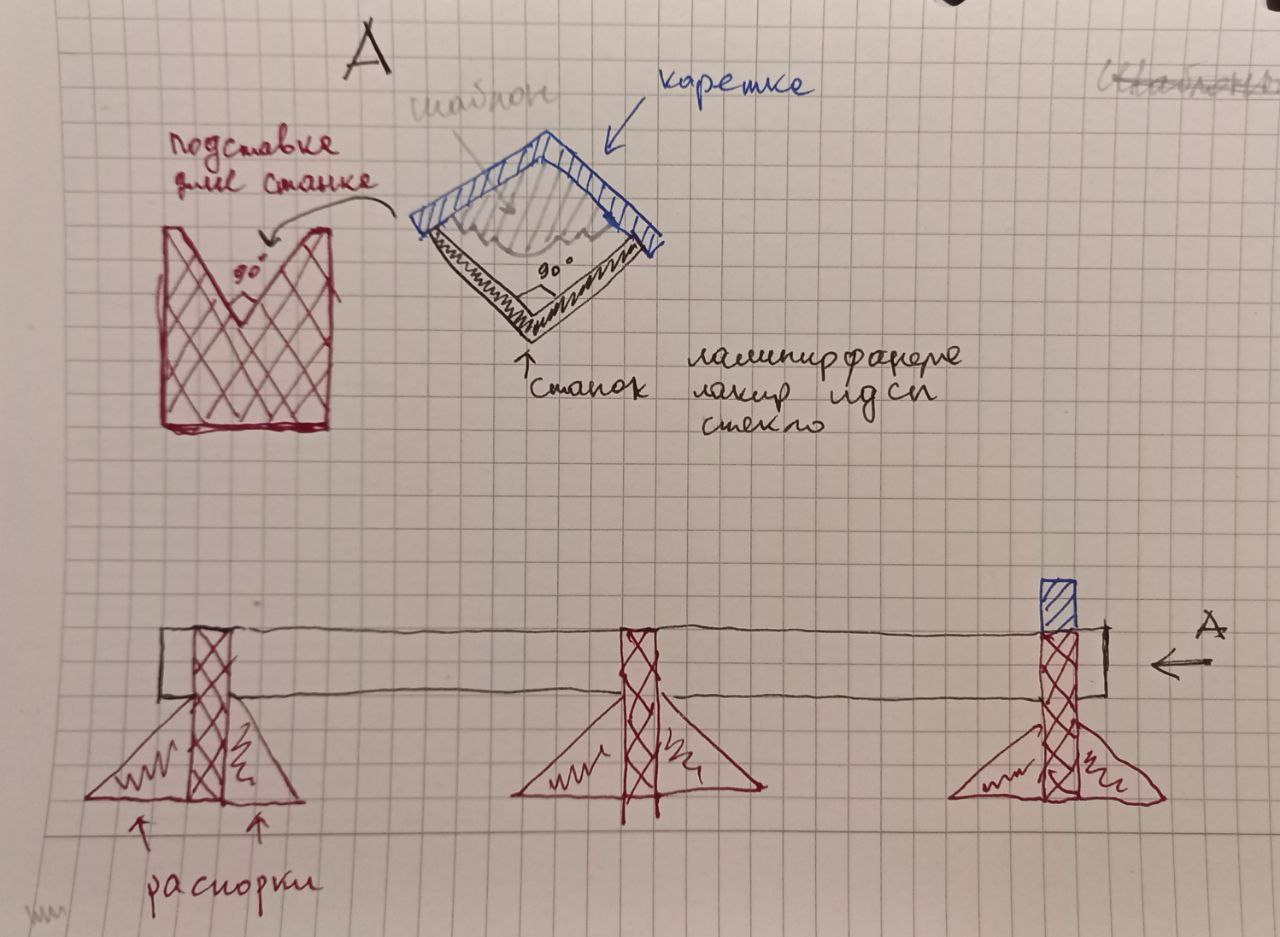 Рисунок 1 - Схема станка для протяжки гипса
Рисунок 1 - Схема станка для протяжки гипса
Станок и подставки
Для изготовления станка рекомендуют брать ламинированную фанеру. У меня её не оказалось поэтому я использовал стенку от старого шкафа. Это ламинированное (или лакированное) ЛДСП. Для моих целей были взяты два куска размером 1700 на 150 мм и скреплены под 90 градусов. Также станок нужно ставить на подставки. Для изготовления подставок берём одинаковые по высоте куски из ЛДСП и выпиливаем в них часть, чтобы поместился станок. Для каждой подставки с двух сторон делаем распорки, чтобы станок не двигался во время протяжки. После того как станок готов можно переходить к изготовлению шаблона и каретки.
Шаблоны
Шаблон будет формировать профиль карниза при протяжке и должен быть закреплён на каретке. Для изготовления шаблона нужен оригинал карниза и чертёж. В моем случае под залог в 1000 рублей выдали образец карниза (кусок размером 20 см). Целиком карниз продавать отказались. Я перенёс контур на бумагу, далее перенес в программу. Нижняя часть (2) это профиль для куклы, верхняя (1) - под карниз.
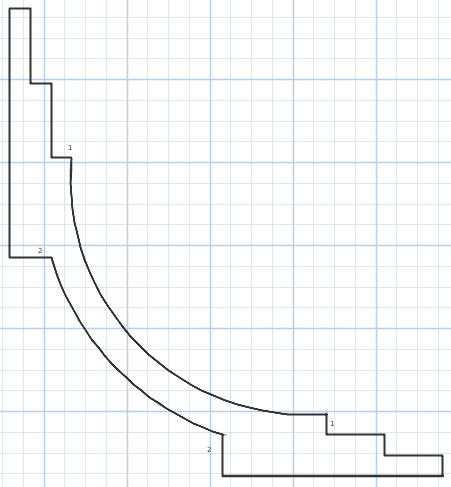 Рисунок 2 - Шаблон карниза
Рисунок 2 - Шаблон карниза
Далее по шаблону нужно вырезать металл. Можно вырезать ножницами по металлу и далее доработать напильником. Но я нашел услугу по резке металла и за 2000 рублей получил 4 варианта шаблонов. Два из нержавейки 1.5 мм и два из обычной стали. Обычная сталь уже успела поржаветь, поэтому рекомендую только нержавейку. Подойдёт и 1 мм и, наверное, даже 0.75.
 Рисунок 3 - Шаблоны из нержавейки (слева) и обычной стали (справа)
Рисунок 3 - Шаблоны из нержавейки (слева) и обычной стали (справа)
Каретка
Каретка это деревянная конструкция, которая будет ездить по станку и формировать профиль карниза. Шаблоны нужно закрепить на каретке. Вначале закрепим шаблон для куклы, а под ней разместим шаблон для карниза. Каретку лучше сделать пожёстче и потяжелее.
Проба пера
Разводим гипс с водой в соотношении 1 к 1. Наливаем полученную жижу в станок, ждём пока начнет схватываться. Берем каретку с шаблоном под куклу и двигаем её вдоль станка. Излишки перекладываем туда, где не хватило гипса и повторяем процесс. Обычно на весь процесс протяжки уходит минут 10-15. За это время гипс схватывается и его уже невозможно тянуть.
После того как кукла готова и высохла ее можно покрыть лаком или краской. Я так сделал, но, наверное, можно обойтись без этого этапа. После лака и перед протяжкой карниза нужно промазать куклу и станок силиконовой смазкой. Я купил сантехническую силиконовую смазку за 300 рублей и доволен результатом.
Протяжка карниза похожа на протяжку куклы, за исключением того, что нужно добиться качества с приемлемыми расходами, так как это конечный продукт. Расход гипса довольно большой, рассчитать точное количество проблематично, особенно вначале и поэтому я выбрасывал чуть ли не 30% от замеса. Большое значение имеет тайминг для протяжки. На первом этапе протяжки карниза важно сформировать профиль гипса, а на втором этапе приготовить замес, которым довести карниз до финала. Второй этап очень похож на первый, но с меньшим количеством гипса и более жидким начальным раствором. Теперь можно разводить не 1 к 1, а добавлять больше воды. Второй этап нужен, чтобы устранить недочеты первого, сформировать углы и придать товарный вид изделию. Иногда мне требовался третий этап, но в идеале обойтись двумя.
Спустя 5 или 6 попыток, которым предшествовали 3 или 4 переделки станка, каретки и доработки шаблона получился вот такой результат.
Снимать карниз после протяжки можно минут через 20-30. Если смазка сработает, то вс пройдет без проблем. Полное высыхание карниза занимает примерно 2 недели. Он побелеет и станет гораздо легче.
Что ещё можно улучшить: 1) Можно увеличить глубину станка, так чтобы шаблон находился глубже. Это позволит не выливаться гипсу за край при протяжке.
2) Увеличить толщину карниза. Это сделает карниз тяжелее, увеличит расход, зато карниз будет крепче и на нем будет меньше трещин.
2) Лучше найти емкости с плоским дном для очистки от гипса после работ. На ум приходит камера от мяча или что-то подобное. Я использую пластиковые бутылки от молока, с отрезанным горлышком, но чистить их затруднительно.
3) Шаблон можно опустить ниже, так чтобы зубья торчали дальше от каретки. Тогда гипс не будет налипать к каретке и будет меньше очистки при проведении работ.
Больше контента в radiopapus
Все фото и видео статьи принадлежат автору. Напишите на почту viktor[cobaka]zharina[tochka]info, если хотите их использовать.
Ссылки:
Прошлые записи
- Комната призвания
- Разбираемся с Coroutine в Kotlin - часть четвертая
- Разбираемся с Coroutine в Kotlin - часть третья
- Разбираемся с Coroutine в Kotlin - часть вторая
- Разбираемся с Coroutine в Kotlin - часть первая
- Отпуск длинною в год
- Подходит ли data class для JPA Entity?
- События как источник правды или как я в стартапе участвовал
- Код 2015 против 2023
- Jvm Internals - Перевод


